Latest FRP Composite Failure Criteria in 2023 for FEA Analysis

FRP Composite Failure Criteria

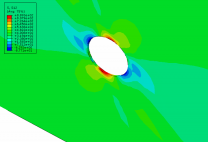
In this blog, I try to review the valid FRP composite failure criteria that have been entered into finite element analysis software (like Abaqus & LS Dyna) so far. Only the failure criteria of intra-laminar failure of composites are examined. In future articles, I will write about interlaminar failure criteria, too.

When we come to the finite element failure analysis in fiber polymer composite laminates (FRP), choosing the appropriate criteria and material model to predict failure and damage is the first question that comes to mind.

Does this criterion have the ability to correctly predict damage and failure in the FRP composite?

How to determine its constants?

Which of the failure criteria has better accuracy?

How about damage evolution?

Etc.

The difficulty of the work can be understood from the fact that according to the definition of  the International Association for the Engineering Modelling, Analysis and Simulation Community (NAFEMS):

There is no universal definition for what constitutes the ‘failure’ of a FRP composite.

However, according to the vocabulary of failure engineering, it is defined as:

‘Failure’ is the point beyond which the structure or component ceases to fulfill its function.

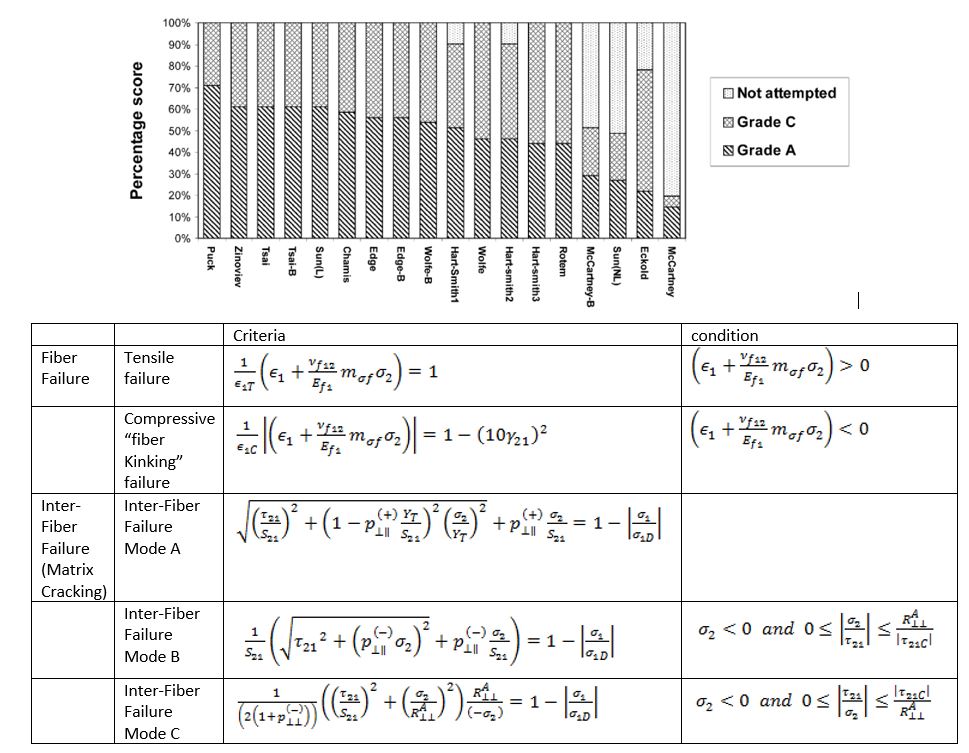
In 2002, Kaddour and Hinton tried to find the best criteria with a global call to ” The World Wide Failure Exercise (WWFE) ” to establish a benchmark for failure criteria because none of the failure and damage criteria and theories were credible for practical engineering applications, .

Fiber Reinforced Polymer Failure Criteria

To perform damage analyses such as impact, a failure criterion is used to determine damage initiation. Fiber-reinforced polymer composite materials have several damage modes, and each mode has its failure criterion. Various failure criteria have been proposed for composite materials; But until now, there is no suitable failure criterion to make an accurate prediction when the stress distribution is complex.

Physical & Non-physical Basis Failure Criteria

The need to predict the failure of FRP composites has led to many theories in this field. Most of the criteria are based on stress and are in the form of an equation or a set of equations. The FRP composite failure criteria classification is not based on a single criterion. Based on the classification done by Echabi and Paris the failure criteria are divided into two categories:

• • Physical basis (related to failure modes), and

• • Non-physical basis (not related to failure modes).

Non-physical basis criteria are expressed using a mathematical relationship and generally in a polynomial form and predict failure by interpolating from several experimental results. In this type of failure criteria, there is no attempt to specify the location or modes of failure.

Non-physical failure criteria are generally expressed in quadratic polynomial form and in-plane stress mode as eq. 1. In the mentioned equation, F_ij and F_j according to the selected criteria and when f=1, failure occurs:

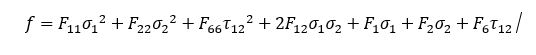
Each failure criterion has tradeoffs in terms of accuracy, conservatism, and complexity. Using both physical and non-physical metrics provides a more robust evaluation of FRP composite performance and failure. The actual failure criteria used will depend on the specific application, tolerable risks, and design philosophy.

Widely Used Failure Criteria for FRP Composite Materials

The most famous and widely used failure criteria for composite materials are:

1. 1. Tsai-Wu Failure Criterion
   2. Azzi-Tsai-Hill Failure Criterion
   3. Tsai-Hill Failure Criteria
   4. Chang-Lessard Failure Criteria
   5. Chang-Chang Failure Criterion
      Similar to Hoffman but includes an interaction term to better model the combined effect of stresses. More accurate than Hoffman.
      
   6. Christiansen Failure Criterion
   7. Feng Failure Criterion
   8. Hart-Smith Failure Criterion
   9. Hashin Failure Criteria
      Separate criteria for fiber and matrix failures under different loading modes (tension, compression, and shear). Require the most material properties but can predict failure accurately under complex loading.
      
   10. Hoffman Failure Criterion
       Failure occurs when the combined effect of longitudinal stress and shear stress reaches a critical value, as defined by the Hoffman equation. Accounts for fiber and matrix failures.
       
   11. LaRC05 Failure Criteria
   12. Maximum Stress Failure Criteria
       Failure occurs when the maximum stress in either the fiber or matrix reaches their respective ultimate strengths. This is a simple and conservative criterion.
   13. Maximum Strain Failure Criteria
       Failure occurs when the maximum strain in the fiber or matrix reaches their respective ultimate strains. Also simple and conservative.
       
   14. Puck Failure Criteria
   15. Yamada-Sun Failure Criterion

The widely used failure criteria range from the simplest (maximum stress/strain) to the more sophisticated multi-axial criteria like Tsai-Wu, Hashin, Puck, Larc05, etc. The simple criteria are easy to apply but less accurate, while the advanced criteria require more inputs but can predict failure more accurately, especially under complex loading conditions.

The most important factors to consider when choosing a failure criterion are:

• • The state of stresses in the laminate
  • The accuracy required
  • The material properties and data available
  • The computational effort and calibration needed

How do the latest FRP composite failure criteria compare to previous criteria?

Interested in developing your own custom failure criteria?

We can help with coding and calculations.

Call us.