VUMAT Subroutine: Shear Anisotropic Modified GTN Damage Model

GTN damage Abaqus VUMAT subroutine

The GTN damage Abaqus VUMAT subroutine is used to model the growth and coalescence of microcracks in materials. This subroutine allows for the implementation of the GTN (Gurson-Tvergaard-Needleman) damage model within the Abaqus finite element analysis software. It is commonly used in the simulation of material failure and fracture in engineering applications.

The VUMAT subroutine enables users to define their own material behavior and failure criteria, making it a powerful tool for accurately capturing the complex damage mechanisms in materials.

What is the GTN damage model?

The Gurson-Tvergaard-Needleman (GTN) damage model is a widely used continuum damage model that describes the behavior of ductile materials under large plastic deformations and failure. It is particularly suitable for materials with voids or inclusions, such as porous metals or polymers.

The GTN damage model considers the presence of voids as the primary mechanism for material failure. It incorporates parameters such as void volume fraction, void shape, and void growth behavior to predict the material’s response under different loading conditions.

The model combines plasticity and damage mechanisms by introducing a damage variable that represents the evolution of voids within the material. The growth and coalescence of voids are governed by damage evolution equations, which are integrated into the constitutive equations of the material.

By using the GTN damage model, Abaqus application engineers can simulate and predict the failure behavior of ductile materials with voids. This information is valuable for designing structures and components that can withstand large plastic deformations and avoid catastrophic failure.

Porous Metal Plasticity Material Model

The ductile damage model and Gurson damage model are the two most popular models used in FE simulation to model the ductile fracture of metal and polymeric materials. The Gurson-Tvergaard-Needleman model is a material plasticity model in which the accumulation of ductile damage is represented by the nucleation, growth, and coalescence of microvoids.
The basic yield function of the GTN model is:

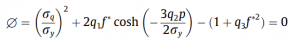
The GTN damage model has a total of nine parameters, which need to be calibrated for a given material. The GTN model is just one model from a particular class of pressure-dependent plasticity models in which the response is dependent on the development of the hydrostatic stress as well as the deviatoric stress tensor. In the model, the micro-voids are represented by a continuous internal variable, the void volume fraction, f.

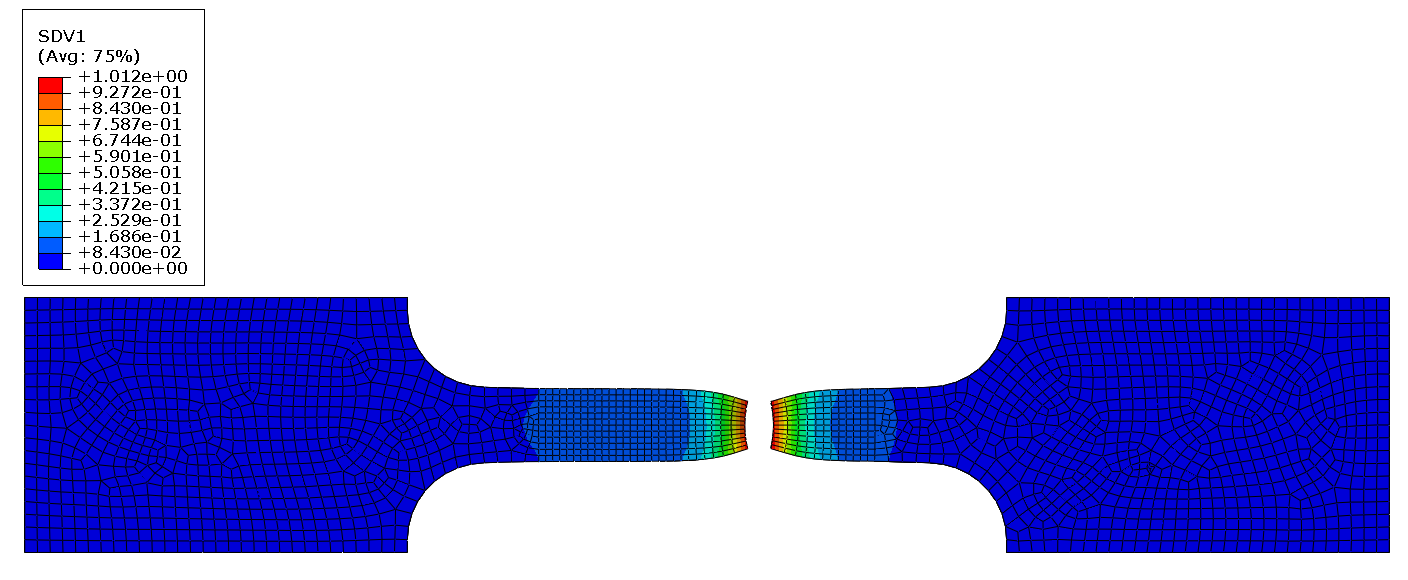
Implementation and validation of modified GTN damage model

The model has been implemented in ABAQUS finite element code via the VUMAT user subroutine. It supports fully the nucleation, growth, and coalescence of voids, and differs from the built-in porous plasticity model provided in ABAQUS/Standard. The modified GTN model has been implemented as a Fortran 90 VUMAT subroutine for use with the Abaqus/explicit.

It has several additional features and offers an alternative to the built-in porous plasticity model in ABAQUS. As well as predicting the void volume fraction, the model calculates the microscopic equivalent plastic strain in the fully dense material, the partitioning of the elastic and plastic strains, and the stress in the material. Integration of the constitutive equations is carried out using the backward Euler method. The incremental forms of the rate equations are nonlinear and coupled together, and robust numerical techniques are required to solve them.

Shear loading

This new advanced Gurson model is proposed, which is an extension of the original to take into account plastic anisotropy and shear loading conditions. The results showed that the modified GTN model improved the modeling accuracy of fracture over the original GTN model under shear loading conditions. Furthermore, the shear plays a role under meridional tensile stress to accelerate fracture propagation in processes such as single-point incremental forming (SPIF). 

In this work, a modified Gurson–Tvergaard-Needleman damage model based on Gatea et al. paper was developed with the consideration of shear to predict ductile fracture in the SPIF process due to void nucleation and coalescence with results compared with the original GTN model in SPIF.  the main motivation of this study is to develop a GTN-based model and to investigate its accuracy and effectiveness in predicting the ductile fracture in SPIF processing of typical truncated cone and pyramid shapes.

In the original GTN model, the increment of void volume fraction is measured based on the nucleation and growth of voids. In this study, the Nahshon-Hutchinson type shear mechanism was incorporated in the GTN model to take into account the effect of shear in the increment of void volume fraction.

Plastic anisotropy

One of the advantages of the Gurson model is its flexibility. Indeed this model can be extended to various mechanical behaviors of the matrix (hardening, plastic anisotropy,…), to many shapes of cavity (ellipsoidal, cylindrical), and several evolution laws of the void volume fraction. These different choices can be combined to generate an enriched or advanced Gurson model. Here, a new advanced model is proposed. This model takes into account plastic anisotropy of the dense matrix which is defined by the Hill anisotropic yield function.

The Hill anisotropic yield function is a mathematical equation used to describe the yield behavior of anisotropic materials. Anisotropic materials exhibit different mechanical properties in different directions, meaning their response to loading varies depending on the direction of applied stress.

The advantages of the modified GTN damage model

• Incorporate plastic anisotropy into constitutive equations of the GTN damage model based on the Benzerga and Besson, 2001 paper by Lankford coefficient.
  
• Consideration of shear to predict ductile fracture and improved the modeling accuracy of fracture over the original GTN model under shear loading conditions based on Gatea et al..
  
• Abaqus application engineers can choose the Mises, Hill, or Barlat criterion independently.

Overview

• VUMAT user subroutine modified GTN damage model for Abaqus software
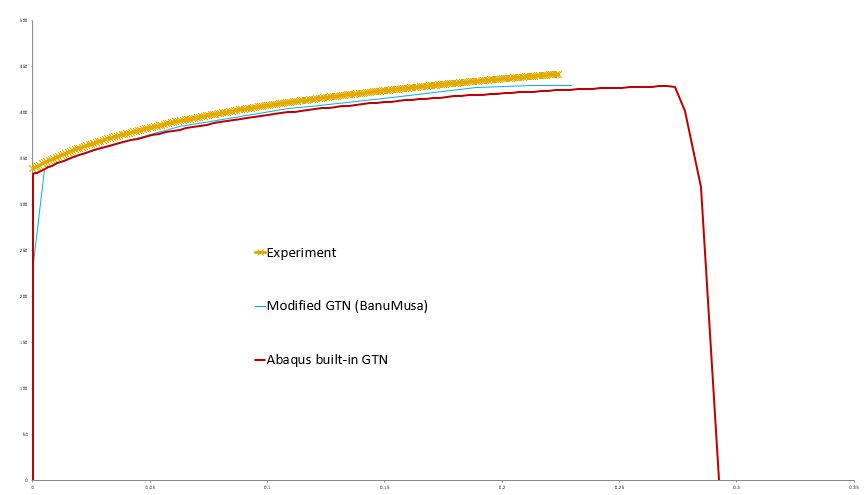
• Example 1: Damage prediction in the tensile test using a shear-anisotropic modified GTN damage model
• Example 2: Damage prediction in the tensile test using Abaqus built-in GTN model (Porous plasticity model)
• Example 3: Damage prediction in the tensile test using an anisotropic-modified GTN model

Abaqus GTN damage parameters

GTN damage parameters for 14 engineering materials to use this criterion are available in Abaqus software. By purchasing this product, you will also receive these material data.

1. Al 6061-T6
2. Pure Titanium
3. AA 6016-T4
4. AA 6111-T4
5. AA 5182
6. AA 6016
7. Al 5182
8. Al 5754
9. Mild steel
10. XES steel
11. ULC/Ti
12. DC 06 steel
13. AA 6016-T4
14. DP 600 steel