In this article, the Hashin damage Abaqus model, 3D Hashin vumat Banumusa code, and 3d Hashin Unifiber code of Simulia are compared. As you probably know, Hashin’s damage model has limitations for Abaqus users in static and dynamic analysis.
For this reason, it is necessary to write a umat/vumat subroutine for it. The good news is that we have already done this and you don’t need to spend a lot of time on it. The efficiency of this code is excellent, you can see the capabilities of this code in the following.
Hashin damage Abaqus model
The anisotropic Hashin damage Abaqus model for unidirectional fiber-reinforced composite is based on the work of Matzenmiller et al. (1995), Hashin and Rotem (1973), Hashin (1980), and Camanho and Davila (2002).
In this damage model, four different modes are considered which include:
- fiber rupture in tension;
- fiber buckling and kinking in compression;
- matrix cracking under transverse tension and shearing; and
- matrix crushing under transverse compression and shearing.
Recently, the LaRC 05 damage model has been added to Abaqus/CAE to predict damage in composite materials.
Damage initiation by Hashin criteria
The Hashin damage Abaqus model defines a damage initiation criterion for composite materials based on the Hashin failure criteria (Hashin and Rotem, 1973 & Hashin, 1980).
The Hashin failure criteria is a set of mathematical equations that predict the failure of composite materials under various loading conditions. The following variables relate specifically to damage initiation at a material point in the FRP composite Hashin damage model:
DMICRT
All damage initiation criteria components.
HSNFTCRT
Fiber tensile initiation criterion.
HSNFCCRT
Fiber compressive initiation criterion.
HSNMTCRT
Matrix tensile initiation criterion.
HSNMCCRT
Matrix compressive initiation criterion.
To display these failure modes, it is necessary to activate these options in the Step module and the Field output.
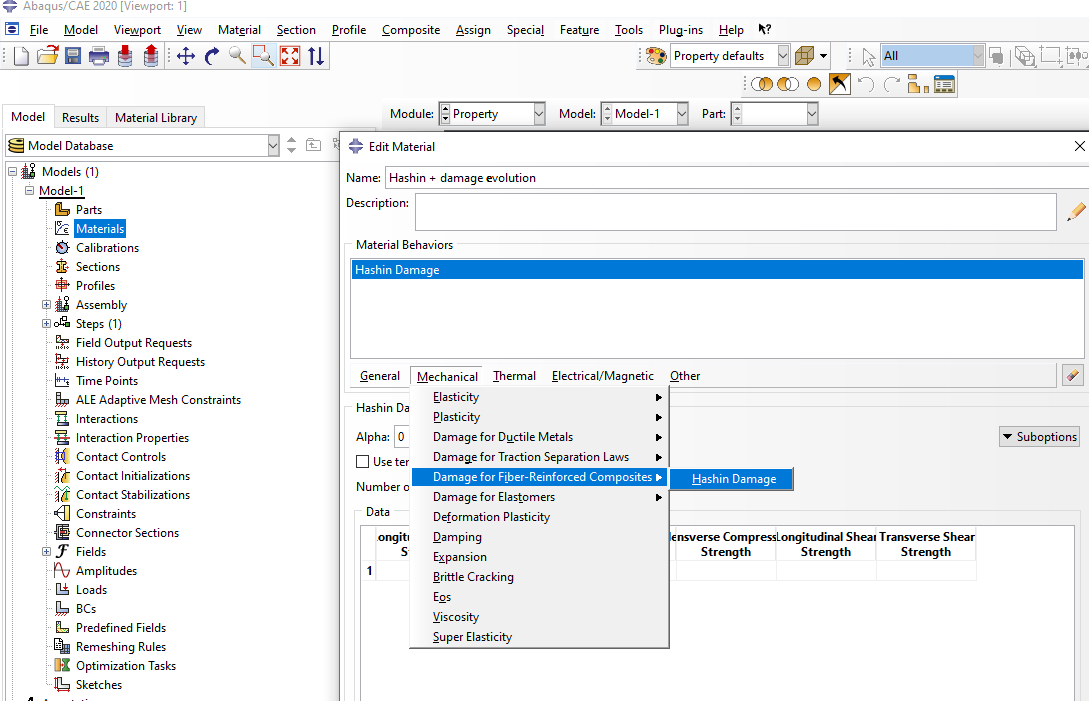
Built-in Hashin damage Model in Abaqus – Damage for fiber-reinforced composites
Damage evolution for fiber-reinforced composites in Abaqus
In composite materials, the behavior of fiber-reinforced composites under damage evolution is a crucial aspect that engineers and researchers need to comprehend. ABAQUS, a powerful finite element analysis software, provides a comprehensive framework for modeling the damage evolution in fiber-reinforced composites.
The damage evolution model in ABAQUS is utilized to capture the post-damage initiation behavior of fiber-reinforced composites. Before damage initiation, the material exhibits linear elastic behavior, characterized by the stiffness matrix of a plane stress orthotropic material. This initial phase sets the foundation for understanding the subsequent damage evolution.
Mesh dependency
To address mesh dependency during material softening, ABAQUS introduces a characteristic length into the formulation, allowing the constitutive law to be expressed as a stress-displacement relation. This approach helps mitigate mesh-related issues during material softening and enhances the accuracy of the simulation.
Element removal
In ABAQUS, when damage variables for all failure modes at all material points reach 1.0, the corresponding element is removed from the analysis. This removal is indicated by setting the STATUS variable to zero for the element. While the element is no longer active and offers no resistance to deformation, it remains visible in the ABAQUS model unless specifically suppressed from display.
It’s important to note that even after removal, the nodes associated with the removed elements still exist in the model. This can lead to non-physical displacements during solution progression, mitigated by adjusting extrapolation settings and being mindful of load application to such nodes.
Viscous regularization
Material models exhibiting softening behavior and stiffness degradation often pose convergence challenges in implicit analysis programs like ABAQUS/Standard. To tackle these issues, ABAQUS offers a viscous regularization scheme that ensures the tangent stiffness matrix of the softening material remains positive for small time increments, thereby enhancing convergence.
Output
Several variables play a crucial role in characterizing and analyzing the damage process in the context of damage evolution in fiber-reinforced composites. These include STATUS, DAMAGEFT, DAMAGEFC, DAMAGEMT, DAMAGEMC, EDMDDEN, ELDMD, DMENER, ALLDMD, ECDDEN, ELCD, CENER, and ALLCD. Understanding and monitoring these variables is essential for gaining insights into the damage evolution behavior within the material.
Key capabilities of ABAQUS for damage evolution
ABAQUS/Standard offers a range of capabilities for modeling damage evolution in fiber-reinforced materials. Some of the key features include:
1. Progressive degradation of material stiffness leading to failure
2. Requirement of linearly elastic behavior for undamaged material
3. Utilization of four damage variables to describe damage for each failure mode
4. Integration with Hashin’s damage initiation criteria
5. Emphasis on energy dissipation during the damage process
6. Options for handling material failure, including the removal of elements from the mesh
7. Possibility of using viscous regularization to improve convergence rate in the softening regime
the following table shows the differences between the built-in Hashin damage Abaqus model and the 3D Hashin VUMAT subroutine developed by BanuMusa R&D.
3D Hashin VUMAT Subroutine vs. Abaqus Hashin Damage
| Abaqus built-in Hashin | 3D Hashin VUMAT Subroutine | |
| Elements | Plane stress, shell, continuum shell, and membrane elements | Three-dimensional solid element |
| Damage Initiation | Hashin and Rotem (1973), Hashin (1980) | Hashin (1980) and Maximum stress criteria |
| Softening Function | Linear | Exponential (based on Linde (2004)) |
| Remove Elements | yes | yes |
| Solver | Standard & Explicit | Explicit |
The 3D Hashin Failure criterion is not supported in Abaqus explicit solver for solid elements; So it needed a 3D Hashin VUMAT Abaqus subroutine to be developed.
The built-in Hashin damage model must be used with elements with a plane stress formulation, which includes plane stress, shell, continuum shell, and membrane elements. so it is not used for 3D solid elements.
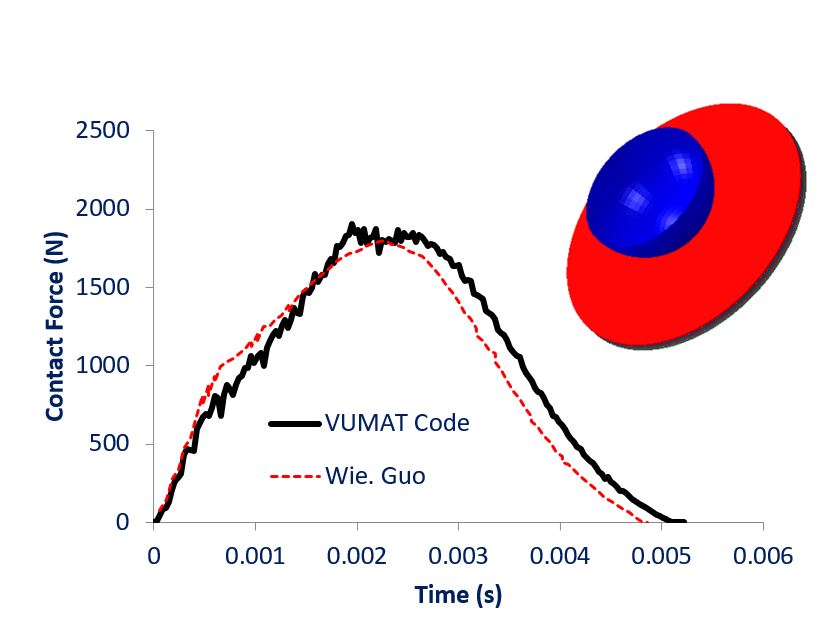
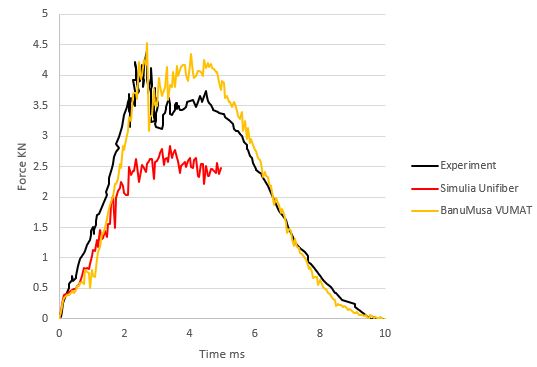
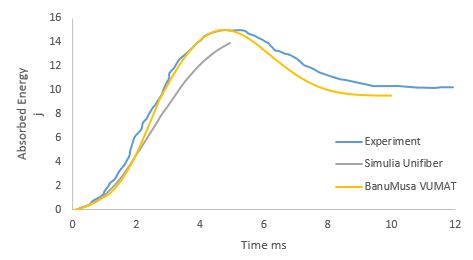
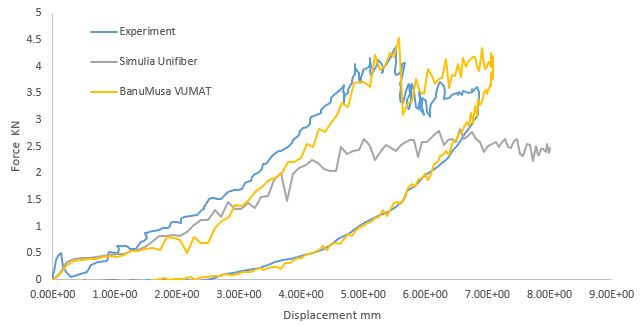
In the following table, the Hashin damage model of Abaqus, the VUMAT subroutine developed by BanuMusa R&D, and the VUMAT subroutine developed by Simulia (Unifiber) are compared in a low-velocity impact analysis. In terms of computational speed, BanuMusa’s VUMAT code had the highest computational speed. The Simulia code did almost half of the solution in 70 hours and the job was not completed. The Hashin Abaqus model required 2 hours more time for complete analysis despite the use of shell elements. 3D Hashin VUMAT of BanuMusa had the least time to solve and the job was completed. All analyses were run on a workstation with a 3 GHz Intel processor with 31 cores.
| Damage Model | Computational time | Softening behavior | Progressive damage | Damage interaction | Shear behavior | Element |
| SIMULIA Unifiber VUMAT | 70 h | No | No | No | No | 3D solid |
| BanuMusa VUMAT | 12 h | Exponential | yes | yes | Maximum stress | 3D solid |
| Abaqus Hashin Damage | 14 h | Linear | yes | yes | No | 2D Plane stress |
3D Hashin BanuMusa VUMAT Subroutine vs. Unifiber subroutine
In the figures below, the comparison of contact force, force-displacement, and absorbed energy for low-velocity impact analysis with two vumat subroutines of Unifiber and BanuMusa are shown. In all three cases, the graphs obtained from the analysis with the BanuMusa vumat code have fewer differences with the experimental laboratory results, which shows the good performance of this code.


 Why do we need a 3D Hashin VUMAT Subroutine?
Why do we need a 3D Hashin VUMAT Subroutine?
The 3-dimensional Hashin damage model is important because it provides a more accurate prediction of the location and extent of damage in composite materials.
Compared to the 2D model, the 3D model considers the influence of through-thickness normal stress components on matrix damage, leading to more realistic failure predictions.
Additionally, the 3D model considers the three-dimensional stress states effect on failure, which is crucial for capturing inelastic deformation and fracture behavior in out-of-plane stress states.
So what is the solution?
Here, we developed a 3D Hashin VUMAT Abaqus Subroutine for that! use it…
 Why do we need a 3D Hashin VUMAT Subroutine?
Why do we need a 3D Hashin VUMAT Subroutine?











nice article